More than Meets the Eye – Neural Networks

As TU20 continues to grow, we would like to recognize some amazing things happening in our community. Every month, we will be featuring one TU20 who has been working on a cool project, initiative or idea. Our goal is to help the writers and readers, grow, learn and connect with each other so they can continue to do great things.

We’re excited to have you join us for our first edition of TU20 Of The Month, and without further ado, I’d like to introduce you to Griffin and his Neural Networks project. Enjoy! 

– Denys

        It may seem like a trivial question – we can instantly recognize this as three “2”s. Yet, if we begin to consider the cognitive processes going on which allow us to recognize these numbers, the true complexity of the question becomes more apparent. My admittedly sloppily drawn twos are very different from one another, especially when compared on a pixel by pixel basis. While viewing each of the images, our brain receives very different sensory input from our eyes. Somehow despite all these differences, we can still effortlessly recognize the digits. If you still don’t see the hidden complexity of my first question, let me illustrate it with this next question – can you write a computer program to recognize those handwritten digits? (Well, that escalated quickly, didn’t it?) If you were like me, you’re probably struggling to think of a practical solution off the top of your head – the shear amount of variance in human handwriting makes this task incredibly difficult. But, as you may have guessed (or maybe you just read the title), a solution does exist – and that solution is machine learning and neural networks.

        As it turns out this is a well documented machine learning problem, which can be considered analogous to the neural network version of a “Hello World” program. But wait, what’s a neural network? Or even machine learning for that matter? Let’s start from the beginning.

        Machine learning is a subset of computer science in which the computer learns how to solve a problem implicitly, instead of having the instructions explicitly given to it. By analyzing vast amounts of data, machine learning algorithms are able to realize statistically significant patterns, which then can be applied to new instances of the problem. As you can see, this approach contrasts greatly with more conventional programming strategies – yet with the massive amounts of data available in recent years (thanks to the internet), coupled with the power of modern computers, it has become a viable and very successful programming approach.

A neural network is a type of machine learning algorithm which is loosely inspired by the structure of the brain. It consists of many artificial neurons, organized into multiple, interconnected layers. Typically, an input is fed into the first layer of the network, which causes neurons in each subsequent layer to “fire”. Similar to the human brain, neurons can have either an excitatory or inhibitory effect on the neurons in the successive layer. After the input signal has propagated through the network, the last layer outputs a value. The network is trained on an enormous amount of training data, where algorithms are used to help the network learn to correct for wrong outputs, until eventually the network can operate on new inputs with impressive accuracy. There are many variations of neural networks, which range in complexity from simple shallow networks, to convolutional deep belief networks. As would be expected, the increased complexity leads to increased potential, which has allowed for some of the great advancements seen in technologies such as voice and image recognition (and many others!).

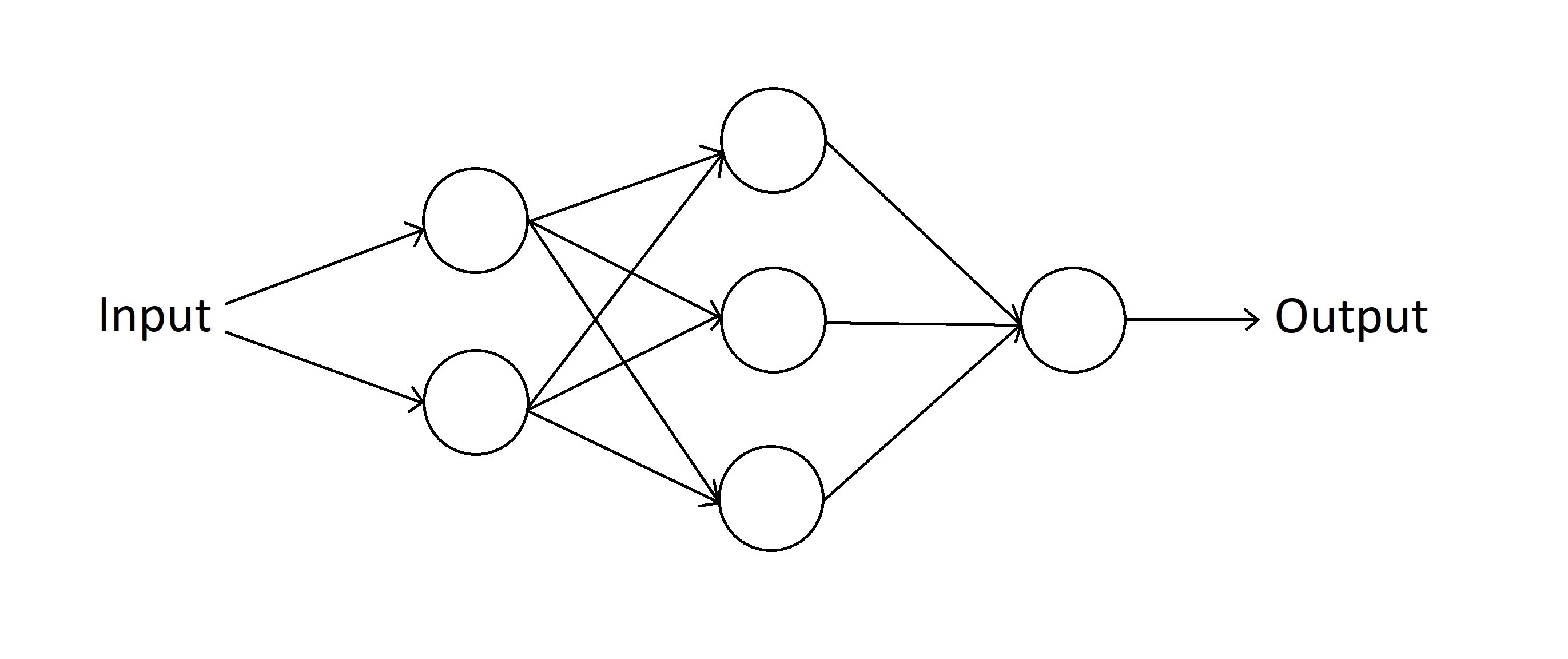
        Going back to our original problem, there is no need for anything too fancy here – a vanilla implementation of a shallow feed forward neural network should do the trick. Furthermore, there are many free datasets available online to train the network with. Because of this, I took this problem as an opportunity to start learning about neural networks. I had been interested in neural networks for a while, and now I had finally found a good starting point to get hands on with them. In order to learn as much from the project as possible, I challenged myself to write the neural network from scratch, without the help of any machine learning libraries. Doing so would develop an understanding of how neural networks work at a fundamental level, which is what I was really interested in.

        The first step of my project was to learn as much as I could about neural networks. Going into the project, neural networks were like a black box to me. I had heard a lot about them due to their hype in the media (you probably have too unless you’ve been living under a rock), but their inner workings were a mystery to me. So in-between studying for my midterms, I spent my time utilizing the greatest resource for self-teaching of the twenty-first century – the internet. Youtube is full of useful videos explaining how neural networks operate at a high level, and for more in-depth information I found that there was an abundance of high-quality online documentation and articles which talked about network layout and training algorithms in detail. After a week or so of reading and note taking, I felt that I had learned enough to start coding. Taking university courses in calculus and linear algebra ended up being very helpful for this project, as those subsets of mathematics are applied heavily in neural networks. I chose to write my code in Python specifically so that I could utilize the math library ‘Numpy’ to optimize the linear algebra powering the network.

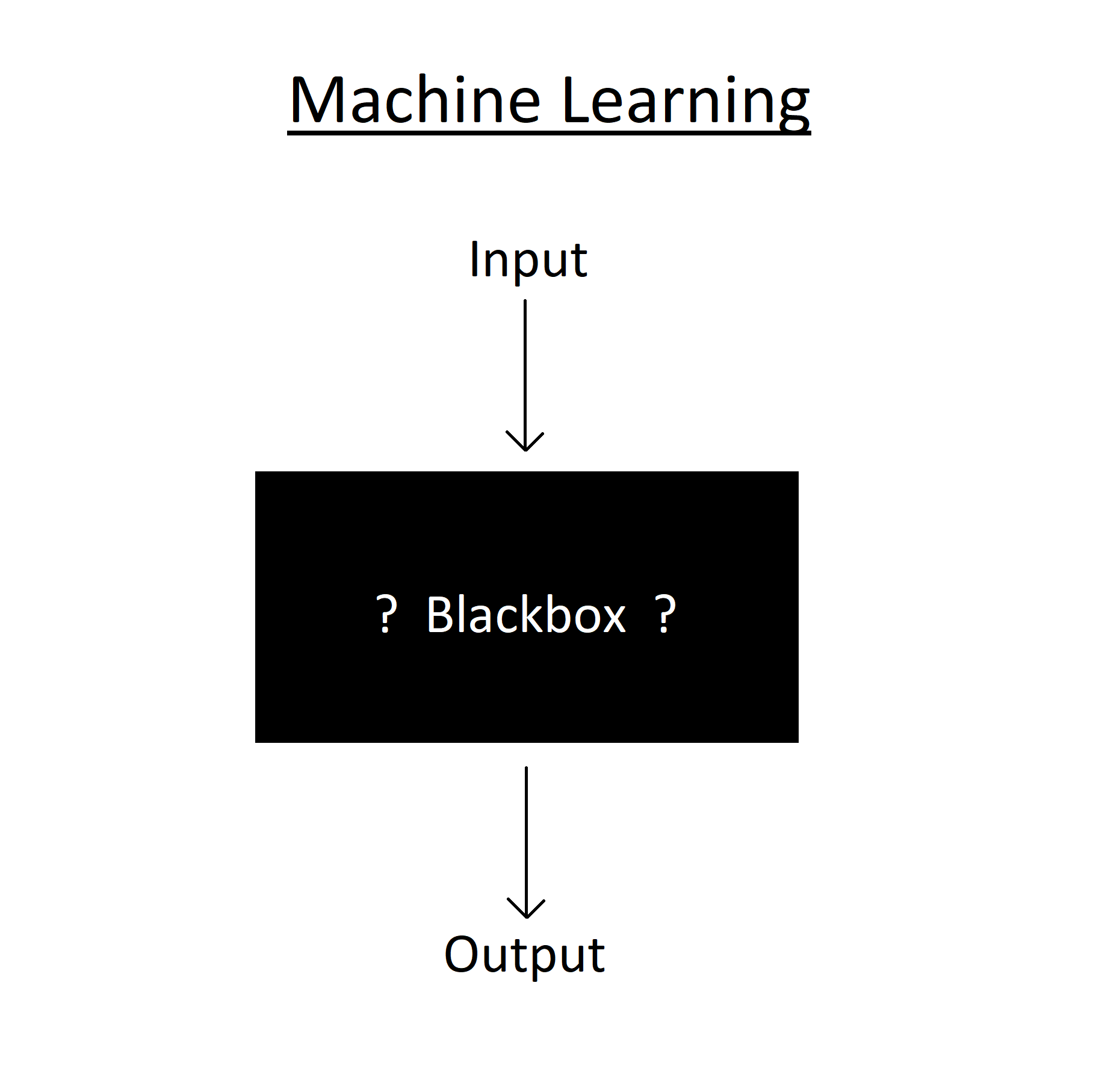
        My first attempt went as most first attempts tend to go – not so well. After eagerly waiting while my network trained itself on fifty-thousand training examples for ten epochs, I was excited to see how well it would perform on my test data. My network ended up classifying the ten-thousand test digits with a whopping seven percent accuracy! That’s about as good as random guessing – obviously something wasn’t right here. After many failed attempts at debugging the code, I decided it was unsalvageable and scrapped it all together. I should mention here that I was so excited to apply the material from my linear algebra class to my program that I ended up jumping the gun: I tried to optimize my network by substituting repeated matrix-vector multiplication with a single matrix-matrix multiplication, but this ended up complicating other aspects of the network, and things got messy. Lesson learned – premature optimization is always a bad idea!

        It was back to square one for my network, but this time I decided to take things slow and just get something working. When my efforts finally paid off, I was ecstatic! I had managed to create a neural network which was able to classify handwritten digits with about ninety percent accuracy. But, I wasn’t ready to stop just yet; now it was finally time for optimization! I optimized my network in four ways, which I will try to explain without getting too technical.

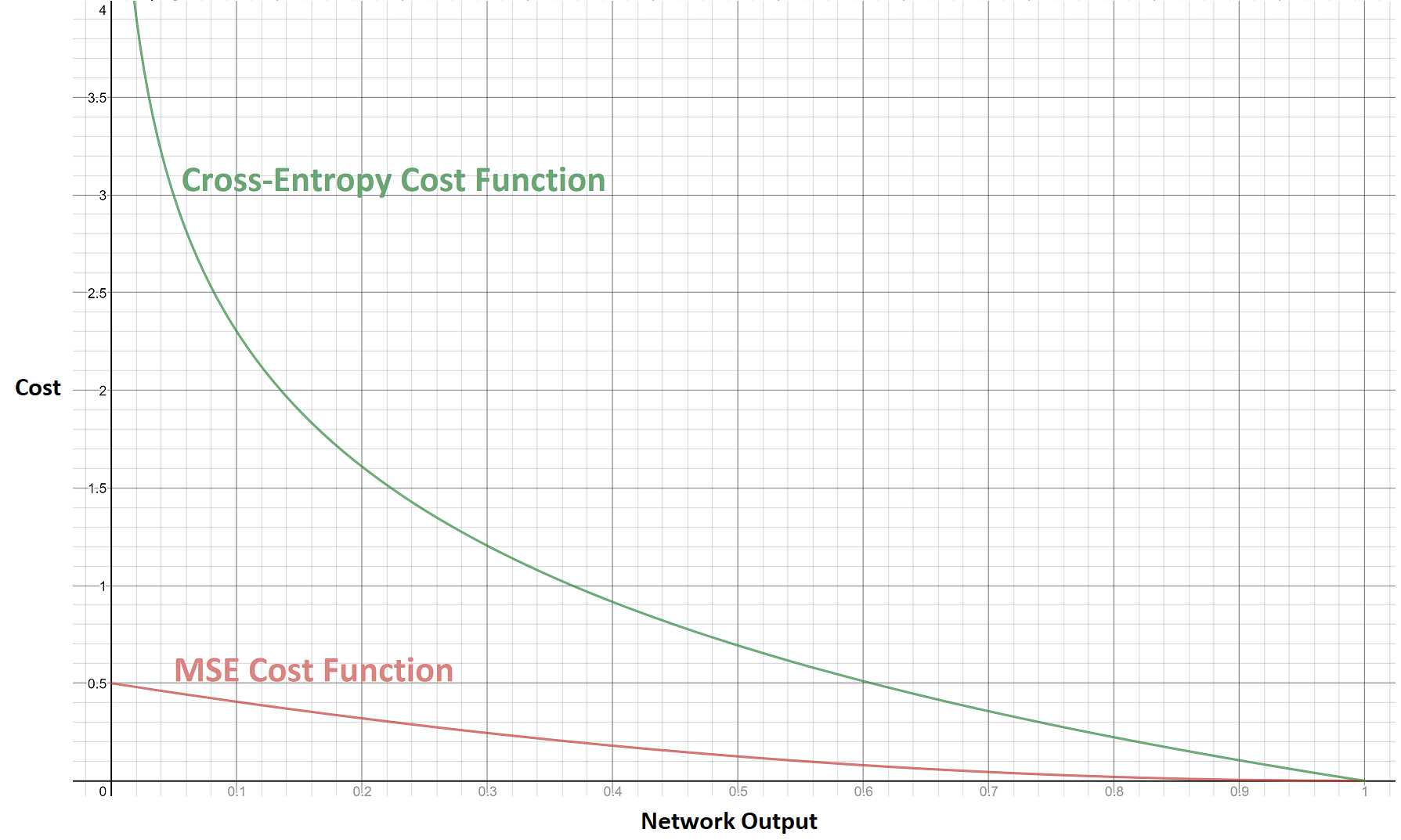
        To begin, I improved the network’s cost function. A cost function is used evaluate how good the network’s output is for any given input – a high cost implies the output is very far from being correct. When the network gets something wrong, the effect that each individual neuron has on the slope of the  cost function is computed, and then the neuron is corrected proportionally. I had originally employed a mean-squared-error (MSE) cost function, yet by replacing it with a cross-entropy cost function, my network was able to learn faster from its mistakes. I have illustrated this below by graphing an example of the two cost functions where the correct output from the network is one. As you can see, when the network’s output is very far from being correct (near zero), the slope of the cross-entropy cost function is much steeper than the MSE cost function.  

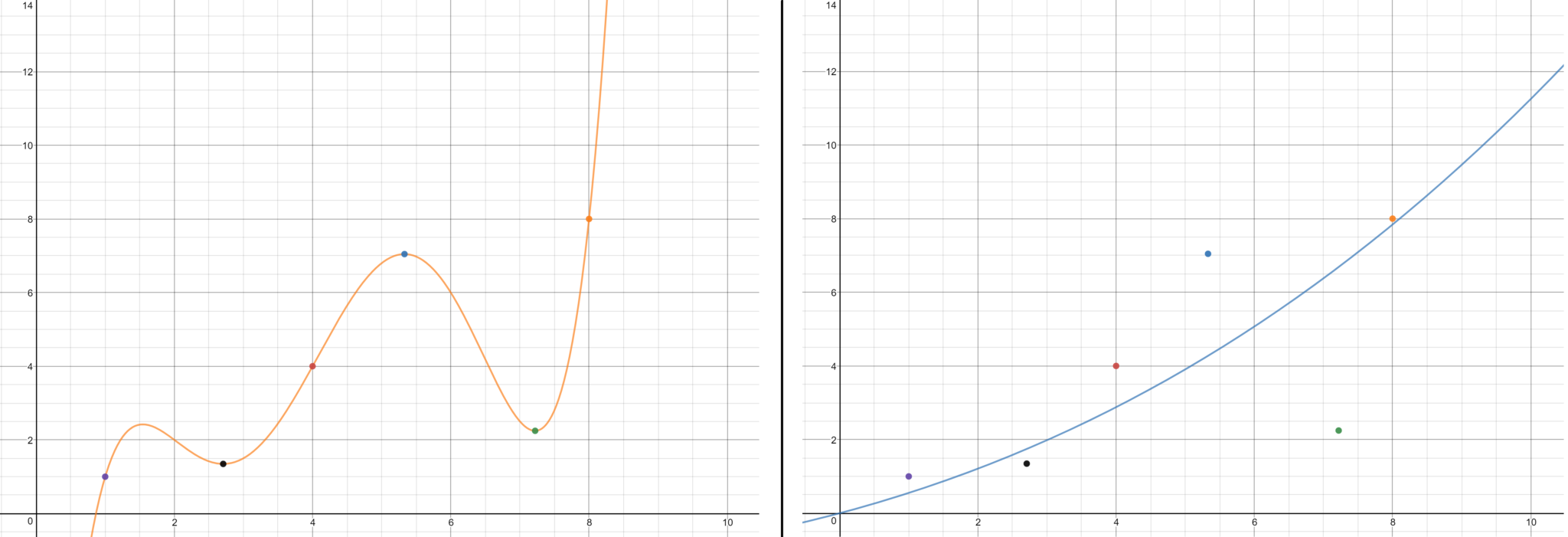
        Secondly, I regularized the cost function using L2 regularization, or weight decay. Regularization is quite a complicated concept, but to explain it in layman’s terms, it is a way to tell the network to prefer simpler solutions instead of more complicated ones, even if more complicated ones are a bit more accurate. Doing so allows the network to better generalize what it learns from the training data to new inputs. A visual interpretation of this can be found below, where I have illustrated two functions (a complicated and simple one) which approximate the values of the points I’ve plotted. As we can see, even though the simpler function (right) is less accurate, it will generalize considerably better than the more complex function (left) assuming that the points continue to follow the upward trend.

        Next, I optimized the starting weights of the connections between the artificial neurons in network. This helps mitigate the amount of saturated neurons in the network before it is trained, allowing it to learn faster initially. To understand why this works, we need to look a little closer at the structure of a neuron in the network. As mentioned earlier, the neurons in a neural network are organized into layers, and these layers are interconnected. More specifically, each neuron in a given layer is connected to every neuron in the previous layer, where each connection is weighted.

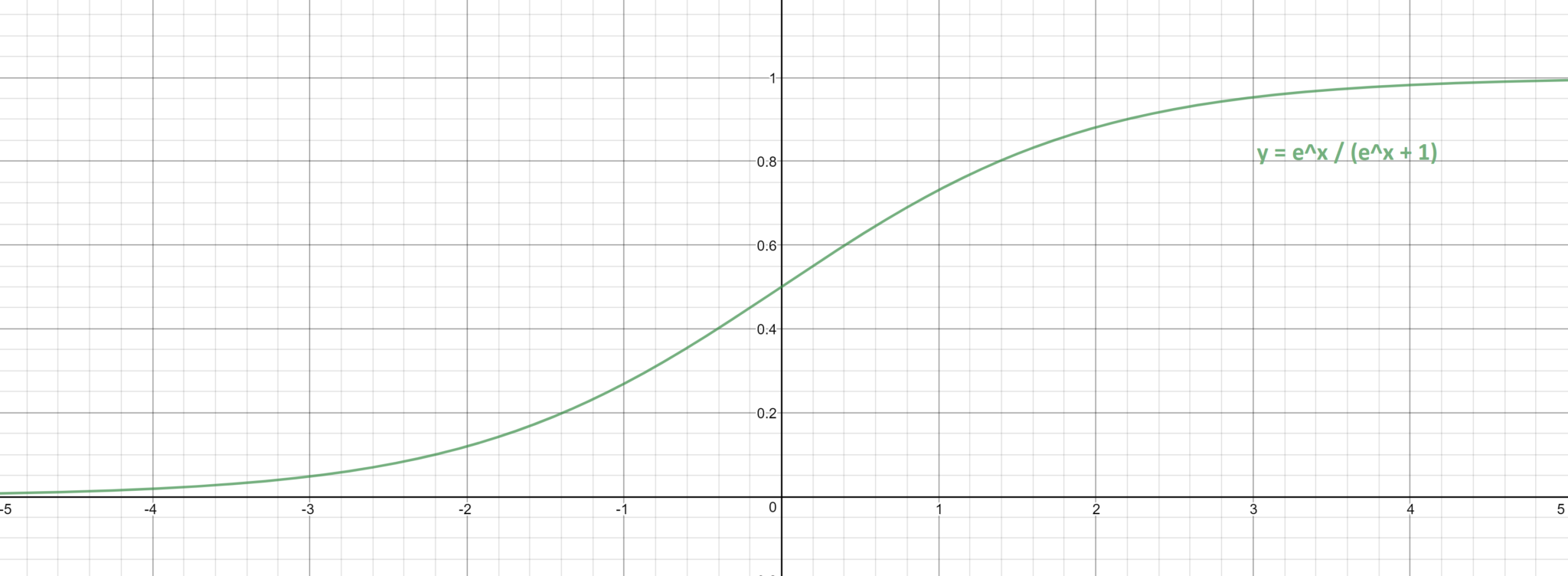
This means that the outputs of the neurons in the previous layer are multiplied by a real number (a weight) before they are fed into the successive neuron. When these weighted inputs are fed into a neuron, the neuron first  passes them through a function, and then repeats the process by passing along its result in the same fashion to the neurons in the next layer. I used sigmoid neurons in my network, which pass the sum of the weighted inputs through a sigmoid function, bounding its resulting non-weighted output between zero and one. Below, I have graphed the sigmoid function. As we can see, when the input to a sigmoid neuron is a very large positive or negative value, the slope of the function becomes very flat. When this happens, we say that the neuron has become saturated, and it will be resistant to change, causing the network to learn slower. By optimizing the starting weights of the network, I can try to reduce the chances of saturated neurons being initialized, hence improving the network’s learning rate.

        Finally, I implemented my matrix-multiplication optimization which gave me so much trouble earlier, which sped up the training time! After all this, I was able to get a maximum accuracy of about ninety-eight percent on the test data!

        While working on this project I learned a lot about the basics of neural networks, but I also had a lot of fun in the process. I think the importance of enjoying yourself while learning is often overlooked – so many of us are only focused on the end result, especially when it comes to education. But, as cheesy as this may sound, the journey is just as important as the destination. If you have fun while you’re learning you’re more likely to put in more effort, be able to rebound after failures, and stay curious and continue to learn more in the future. If you’re curious about something, don’t wait to be taught it – be your own teacher, learn something new, and have fun. I’ll end by asking you one final question: what’s your next project going to be?

That’s some exciting stuff Griffin !

To all our readers, hopefully after reading this article, you are more knowledgable about Machine Learning and Neural Networks, and will continue to explore the area on your own.

If you know someone who is doing some great stuff within the community, please reach out and let us know!

Send us a message on social media or at techunder20 (at) gmail (dot) com! Enjoy the rest of your weeks, and we’ll see you next Month!

– Denys